앞에서 4자유도 로봇팔을 제어하기 위해, Forward Kinematics순기구학 풀이법을 알아보았습니다.
[로봇 이론/Robotic Arm] - 4DOF Manipulator 로봇 팔의 운동학(기구학) 이론(2) ㅡ Forward Kinematics (순기구학, 정기구학)
- Denavit-Hartenberg 매개변수
- Forward Kinematics 해를 결정하기 위한 좌표 변환
- 4DOF Manipulator Forward Kinematics 계산
- Product of exponentials
4자유도 매니퓰레이터 변환 행렬은 다음과 같이 표현되었습니다.

이제 드디어, end effector의 위치나 자세(주어진 변환)로부터 각각의 관절의 자세(각도)를 알아낼 수 있는 Inverse Kinematics역기구학에 대해 알아보겠습니다.
Inverse Kinematics(역기구학, 역운동학)
- 2DOF Manipulator 역기구학 풀이
- 3DOF Manipulator 역기구학 풀이
- 4DOF Manipulator 역기구학 풀이
Inverse Kinematics(IK)의 풀이는 분석적인 방법과 수치계산적인 두가지 방법으로 나뉠 수 있습니다. 또, 주어진 end effector의 위치로부터의 각각의 관절의 각도의 해는 무수히 많을 수도, 존재하지 않을 수도 있을것입니다. 대부분 분석적인 방법의 해법은 해가 보통 존재하지 않으며, 유일한 해도 아닙니다.
6자유도의 일반적인 로봇에는 역기구학의 closed-form solution이 없지만, 풀 수 있는 특수한 경우가 있는데,
3개의 연속 축이 한 지점에서 교차하면 역기구학의 해가 언제나 존재한다는 파이퍼(Pieper)의 solution이 있습니다. 이 솔루션은 현재 상업적으로 이용가능한 산업용 로봇에 널리 쓰이고 있습니다.
- Piper's solution
앞의 3개 관절이랑 뒤의 3개 관절을 분리하여,
앞의 관절 3개는 위치(x,y,z)를 조절하고, (위치 변환)
end effector 부분에 마지막 관절 3개의 축들을 한점에서 위치시키면, 마지막 관절 3개는 각도를 담당하게됩니다. (회전 변환)
제가 풀고자 하는 것은 closed form이 있는 2DOF와 3DOF Manipulator Inverse Kinematics이고,
몇가지 제한적인 상황에서 해를 가지는 4DOF Manipulator의 IK풀이입니다.
2DOF Manipulator 역기구학 풀이
2자유도 매니퓰레이터(로봇 팔)의 Inverse Kinematics의 해는 구조상 0개이거나, 2개입니다.
다만, 특수한 경우 1개인경우가 있는데, 각 링크의 길이의 합과 끝 점의 위치(x,y)가 원점으로부터 떨어진 거리와 같을때, 즉, 로봇팔을 일자로 했을 때의 해 하나가 있다는 것을 생각해볼 수 있습니다.
동차 변환이 다음과 같이 주어졌을 때,

이 식에서, ϕ각은 𝛳1+𝛳2이어야합니다.
즉, ϕ=𝛳1+𝛳2
이는 2관절 매니퓰레이터 계산에 필요한 다음 그림들을 보면 이해하기 쉽습니다.(Geometric approach)
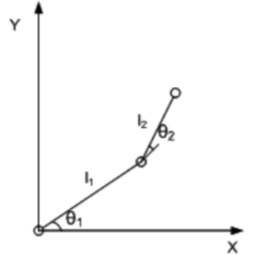
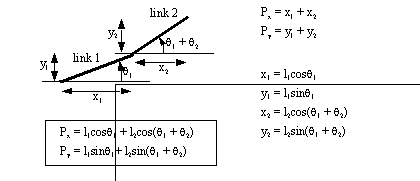

위의 식과 그림으로부터, 끝의 x좌표와 y좌표는 다음과 같이 표현 됩니다.

위의 식을 제곱하여 더하면, 다음과 같습니다.

이로 인해 각도𝛳2를 구할 수 있습니다.
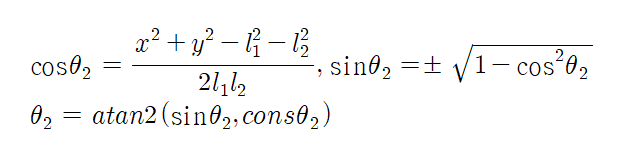
*참조. atan2 함수는 tanθ의 역함수 arctan(y/x) 임.

s𝛳2의 부호를 선택해야 하는 것은 두개의 해가 존재한다는 것이고, 관절각이 위로 올라가거나 아래로 내려가는 것을 의미합니다.
𝛳2를 구하게 되면 𝛳1도 구하기 위해 식을 정리합니다.


이러한 형태의 수식을 풀기 위해서는 변수를 바꾸어 다음과 같이 풀 수 있습니다.




이렇게 𝛳1값도 구해집니다.

k값을 정리해 다시쓰면, 다음과 같습니다.

따라서, 끝점의 좌표로부터 두 관절의 각도 𝛳1,𝛳2 를 구하는 순서대로 쓰면 다음과 같습니다.


3DOF Manipulator 역기구학 풀이
앞의 2DOF Manipulator에 관절 하나를 추가한 3자유도 Manipulator에 대해 생각해 보겠습니다.
추가된 축은 앞의 2자유도 Manipulator와 평행한 z축을 가지도록 하여 같은 차원(x좌표, y좌표)을 가집니다.
앞선 2DOF Manipulator를 확장한것 뿐이고, 3차원은 하나의 축을 더 추가하여 본래의 목적인 4DOF를 통해 계산할 것입니다.

위와같은 3DOF 매니퓰레이터의 Forward Kinematics 식:

위 식을 역시 더하고, 스퀘어링하고, 나누고, 삼각함수 공식을 사용하면 Inverse Kinematics 식을 다음과 같이 구할 수 있습니다.




주목할 것은, ϕ는 x(혹은 ground)축과 end effector사이의 각도라는 점입니다.

3자유도 매니퓰레이터의 경우 로봇 팔 끝부분을 위치시키기 위한 링크 각도의 해가 무수히 나올 수 있습니다.
따라서 추가적인 조건이 있어야 각도 선택이 가능합니다.
마지막 링크의 각도(θ₃)를 x축(또는 밑 평면)과 평행(0,π)하거나, 수직하게 하는 등(π/2) 조건을 달수 있고,
각각의 링크의 각도 또한 자연스러운 움직임을 위한 각도 범위를 두어 해를 구하는 것이 좋습니다.
4DOF Manipulator 역기구학 풀이
제가 풀고자 하는 4DOF Manipulator 역기구학은 위의 3DOF Manipulator에 밑의 그림과 같은 관절을 하나 추가하여 3차원의 Manipulator입니다.
- ϕ = 0 인 경우

마지막 링크의 각도(θ₃)를 밑의 평면과 평행하게 두었고, (즉, ϕ = 0.)
θ₁를 추가하여 3차원의 움직임을 하게 되었습니다.
위 그림에서, θ₁은 비교적 간단하게 구할 수 있습니다.

또한 각각의 나머지 각도는 위의 3DOF Manipulator Inverse Kinematics풀이와 다르지 않습니다.
나머지 3관절을 하나의 xy평면(2차원)으로 보면 됩니다.
그럼, y축을 기준으로 회전하여 x축이 변하게 되는데,
이때의 변화된 x축에 따른 x의 값도 구할 수 있습니다.

그럼, 위의 3자유도 매니퓰레이터 공식을 변화된 x에 맞게 바꿔주기만 하면 됩니다. (유레카!)

- ϕ = 90 인 경우
이어서 작성.
'로봇 > Robotic Arm' 카테고리의 다른 글
| Forward Kinematics (순기구학, 정기구학) ㅡ 4DOF Manipulator 로봇 팔의 운동학(기구학) 이론(2) (4) | 2020.01.17 |
|---|---|
| 강체의 수학적 표현: 회전 행렬, 오일러 각도, 롤피치요 각도, 동차 변환 ㅡ 4DOF Manipulator 로봇 팔의 운동학(기구학) 이론(1) (6) | 2020.01.14 |

